研究室紹介OPAL-RING
川端 研究室
多次元漸近的量子化、特異確率測度に対するレート歪理論、
データ圧縮アルゴリズムの設計と解析
| 所属 | 大学院情報理工学研究科 情報・通信工学専攻 |
|---|---|
| メンバー | 川端 勉 教授 |
| 所属学会 | 情報理論とその応用学会、電子情報通信学会、IEEE、日本応用数理学会 |
| 研究室HP | http://www.ict.cei.uec.ac.jp/kawabata/ |
| 印刷用PDF |
掲載情報は2015年8月現在

- 川端 勉
Tsutomu KAWABATA
- キーワード
-
漸近的ベクトル量子化、情報源符号化、格子、微分幾何学、レート歪関数、特異確率測度、レート歪次元、木情報源、Lempel-Ziv符号、文脈木重み付け法
研究概要
情報源符号化の研究
通信の目的は通信路を介して情報源の出力を受信者に伝送することである。情報源の出力の例としては、音声符号などの連続時間信号X(t)やテキストファイルなどの離散時間離散値データXnがある。
情報通信の第1段階は情報源出力の2進記号(0と1)を用いた符号化であり、その目的は電子文書、画像、音といった様々なデータの見かけの情報量を圧縮することである。このため、これを情報源符号化あるいはデータ圧縮とも言う。情報源符号化により、通信は通信路を介した情報伝送問題に帰着され、単純化される。また情報源符号化の理論は情報伝送問題を含む様々な問題の基礎となる。
無歪み情報源符号化の研究
情報源符号化ではテキストファイルのように歪みのない復号が可能な場合と、連続信号のように本質的にそれが不可能な場合がある。そこでまず可能な場合について考えてみる。もしXnが確率法則に従うならば、符号化の出力である2進列の長さの期待値を考えることができる。この期待値をあらゆる符号化に関して最小化できれば、その最小値こそ情報源の持つ本質的な情報量と言えるだろう。
では確率法則が存在するとした場合、本質的な情報量の値をXn自身から推定することは可能だろうか。仮定の話ではあるが、もしそれが可能ならば、算術符号化法という実数の数変換に対応する技術を用いて推定値に付随する符号化法が得られると考えられるのである。一方、Xnがテキストファイルの場合は、木情報源という階層的な確率法則の族が標準的だと考えられている。
木情報源、文脈木重み付け(CTW)法、Lempel-Ziv符号化法
当研究室では、木情報源に対して有効な推定法である文脈木重み付け(CTW)法について研究している。
さて木情報源の仮設に計算量的な無理がある場合は、本質的情報量に至る別の道が必要となる。
当研究室では、その場合に有効と考えられるLempel-Ziv符号化法(辞書法)について設計ならびに圧縮性能解析の両面から研究をしている。
以下では増分分解法と呼ばれる方法のアルゴリズム設計に関する研究を手短に紹介する。この方法は空の辞書ならびに符号化すべき文字列から出発する。方法は極めて単純であり、入力文字列の先頭から辞書の中にない最短の語を見つけてはそれを切り取り、切り取った語を辞書に登録するという手続きの繰り返しに基づいている。新しく切り取った語は既に辞書に登録されている語に1文字付け加えたものであるので、短い表現(すなわちデータ圧縮)が可能となるのである。
当研究室では、この基本的方法に対して、新しい分解語を辞書のもつ木構造の中で効果的に数え上げて表現する技法を開発した。この方法は極めて短い手続きで記述できるだけでなく、もともとの方法にあったいくつかの欠点を帳消しにする性質の良い方法である。また開発された方法は、増分分解法を越えた広い応用があり、未だに発展中である。その意味でも基本的技術であると言える。
この方法の提案は、当研究室が従来から行ってきた解析的研究の副産物であると考えている。
有歪み情報源符号化の研究
次に、信号歪みを許容する場合を考えてみる。この場合も情報源の確率法則の仮説のもとで符号化の効果、すなわち情報圧縮レートと許容歪みのトレードオフ関係を調べることが重要な課題となる。
しかし、この関係は信号の種類に大きく依存する。
たとえば、現実の信号には連続信号でも離散信号でもない特異な信号が現れる。この場合には理論の空白状態があった。
だが、当研究室ではフラクタル信号を含む特異信号に対する圧縮率歪み関係を発見した。
情報理論において、この理論は連続でも離散でもない特異信号に対する圧縮理論という情報理論の新しい世界を切り拓いたのである。
アドバンテージ
数理工学に基づく独創的研究
情報理論は、情報通信の理論的基礎を成す電気電子情報系の学問であり、工学的実現を最も重視している。よって、先進的研究に取り組むには基礎が大切である。
当研究室では、その基礎をすでに体系化されている情報理論だけではなく、数理統計学や幾何学的方法など数理工学にも置いているので、独創的なアルゴリズム設計やシステム解析法の研究が実践できている。
一例を挙げたい。80年代末ヒトゲノム計画が企画され、その中でDNA塩基配列の検索需要の急増が予想された。検索の方法として、並んだ塩基配列の近さを塩基対間定義したスコアの和と定義し、部分列の両端を変えてこの和の最大値を考え、それが並びをスライドさせたときにさらに最大となる位置を探す方法が考えられた。
この方法はAltschulによりBLAST法として実現され、当時はもちろん現在も使われている。統計解析は同時進行で、スタンフォード大においてKarlin、Dembo、川端により行われた。このためBLAST法はKarlin-Altschul法ともよばれている。
情報理論の拠点:電気通信大学
デジタル通信の技術開発に携わる技術者が長く、第一線で有意義に活躍するには、長期的視野が必要であり、それを与えてくれる基本原理が情報理論である。情報理論は、直接間接に様々な科学・工学領域の基礎にもなっており、様々な研究経験を経て、情報理論にたどりつく研究者も少なくない。電気通信大学は、その情報理論における日本のメッカであり、当研究室では、本学で教えられる情報理論を核に、先進的な情報通信技術を学ぶ事ができる。
今後の展開
2段階量子化方式の改善に挑戦
歪みを許容する場合(ベクトル量子化法)の研究をもう1つ紹介する。連続信号の高解像度圧縮の問題は、多次元漸近的量子化問題として研究されている。これは空間における多点配置問題に等価である。
当研究室では、今まで見捨てられてきた2段階量子化方式を再発掘し、理論と方式の改善を試みている。これが実現されると、これまで使われてきた標準方式(一様量子化法を経て可変長に符号化する方式)が一変してしまうことになるだろう。
最後に、情報源符号化は通信における秘匿性の向上のために有効であることが議論できる。秘匿性の向上、あるいは情報ハイディング理論は、今後の有望な応用領域といえる。
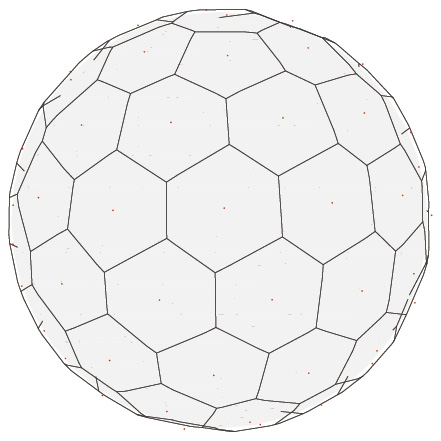
- 2段階量子化研究の一環として設計した球面の量子化器

- ゼミでは既成概念に縛られることなく、
自由に様々な意見が飛び交う

